Question

The mayor of a town has proposed a plan for the annexation of a new community. A political study took a sample of 900 voters in the town and found that 76% of the residents favored annexation. Using the data, a political strategist wants to test the claim that the percentage of residents who favor annexation is above 73% . Make the decision to reject or fail to reject the null hypothesis at the 0.10 level.

Answer 1

Reject the null hypothesis

Explanation:

The proportion of t voters in the sample of 900 voters that favored annexation is 76% = 0.76, so we can estimate the standard deviation as

`\bf s=√(900*0.76*(1-0.76))=12.812`

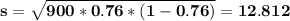
The mean according to the sample is 76% of 900

`\bf \bar x_a`= 0.76*900 = 684

The stated mean is 73% of 900

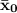`\bf \bar x_0`= 0.73*900 = 657

We have then the hypothesis

`\bf H_0`: The mean is 657

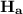`\bf H_a`: The mean is greater than 657

This is a right-tailed test.

Our critical value at the 0.10 level is

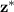`\bf z^*` = 1.282 (The area of the Normal N(0,1) for z > 1.282 is less than 0.10. This value is obtained with tables or computer)

The zone of rejection is z > 1.282

Our z-statistic is

`\bf z=(\bar x_a -\bar x_0)/(s)=(684-657)/(12.812)=2.107`

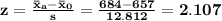
Since 2.107 > 1.282 we reject the null hypothesis.