Question

Construct an argument that shows that the set of rational numbers is closed under division. That is, if x and y are

rational numbers (with y nonzero) and ???? = x / y' prove that ???? must also be a rational number.

Answer 1

`(x)/(y)` can also be expressed as a ratio of two integers.

Explanation:

Assume x and y are rational number, then x and y can be written as:

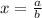`x=(a)/(b)`, where a and b are integers and b≠0

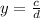`y=(c)/(d)`, where c and d are integers and d≠0

Then,

`(x)/(y)` =
`((a)/(b) )/((c)/(d) )`

=
`(a*d)/(b*c)`

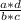
Since the set of integers are closed under multiplication, a*d is also an integer. Similarly b*c is also an integer.

`(x)/(y)` can be expressed as a proportion of two integers, provided that y≠0. From this we can conclude that
`(x)/(y)` is a rational number, which concludes that the set of rational numbers are closed under division.