Answer:
Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. There is a 48.67% probability that he voted in favor of Scott Walker.
Explanation:
We have these following probabilities:
A 53% probability that a respondent voted in favor of Scott Walker.
A 100%-53%=47% probability that a respondent voted against Scott Walker.
If a respondent voted for Scott Walker, there is a 37% probability that he had a college degree.
If a respondent voted against Scott Walker, there is a 44% probability that he had a college degree.
Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. What is the probability that he voted in favor of Scott Walker.
This is the percentage of those who have a college degree and voted for Scott Walker divided by the percentage of those who have a college degree.
Percentage of those who have a college degree.
53% voted for Scott Walker. Of them, 37% have a college degree.
47% voted against Scott Walker. Of them, 44% have a college degree.
So:
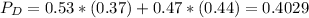
Percentage of those who have a college degree and voted for Scott Walker.
53% voted for Scott Walker. Of them, 37% have a college degree.
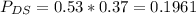
So
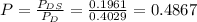
Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. There is a 48.67% probability that he voted in favor of Scott Walker.