Answer:
1. It is a rational function.
2.
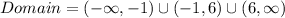 .
.
3. End behaviors are shown below.
4. Vertical asymptotes : x=6 and x=-1; horizontal asymptote : y=0.
Explanation:
The given function is
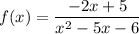
1.
A ration function is defined as
f(x)=p(x)/q(x)
The given function is in the form of p(x)/q(x).
Therefore, it is a rational function.
Find the factors of denominator.

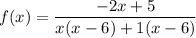

Equate the denominator equal to 0.

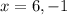
Therefore, the function is not defined for x=6 and x=-1.
2.
The domain of given function is all real number except 6 and -1.
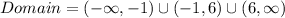
3.
End behavior of the function.
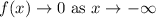
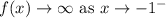

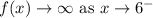
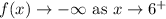
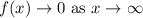
4.
To find the vertical asymptotes we need to find the zeroes of the denominator.
The vertical asymptotes of the function are x=6 and x=-1.
If degree of denominator is more than degree of numerator, then the horizontal asymptote is y=0.