Question

Does the graph of the function f(x) = x^2 − 8x − 9 / x + 1 have a vertical asymptote or a point missing at x = −1? Explain

your reasoning, and support your answer numerically.

Answer 1

Yes, the graph of the function has vertical asymptote at x=-1.

Explanation:

Given : Function
`f(x)=(x^2-8x-9)/(x+1)`

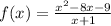
To find : Does the graph of the function have a vertical asymptote or a point missing at x = −1?

Solution :

The vertical asymptote of the rational function is when we put denominator equals to zero.

In the function
`f(x)=(x^2-8x-9)/(x+1)`

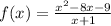
Denominator -
`x+1`

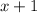
Vertical asymptote is at
`x+1=0\Rightarrow x=-1`

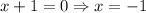
Yes, the graph of the function has vertical asymptote at x=-1.