Answer: 2.3425
Explanation:
As per given , we have
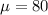
n = 20
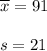
We assume that the population is approximately normally distributed.
Since population standard deviation is unknown , so we use t-test.
Test statistic :
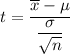
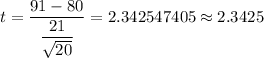
Hence, the calculated value of test statistic = 2.3425