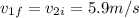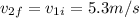Question

In an elastic collision, a 300 kg bumper car collides directly from behind with a second, identical bumper car that is traveling in the same direction. The initial speed of the leading bumper car is 5.30 m/s and that of the trailing car is 5.90 m/s. Assuming that the mass of the drivers is much, much less than that of the bumper cars, what are their final speeds (in m/s)?

Answer 1

If we had:

`v_(1i)=5.3m/s`

`v_(2i)=5.9m/s`

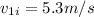
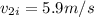
We will have:

`v_(1f)=5.9m/s`

`v_(2f)=5.3m/s`

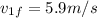
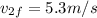
Step-by-step explanation:

In an elastic collision both linear momentum and kinetic energy are conserved, so we will have:

`p_i=p_f`

`K_i=K_f`

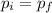
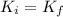
We will call our bumpers 1 and 2.

For the momentum equation we know that:

`m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)`

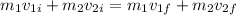
Since all the masses are the same (300kg), they cancel out:

`v_(1i)+v_(2i)=v_(1f)+v_(2f)`

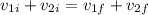
For the kinetic energy equation we know that:

`(m_1v_(1i)^2)/(2)+(m_2v_(2i)^2)/(2)=(m_1v_(1f)^2)/(2)+(m_2v_(2f)^2)/(2)`

Since all the masses are the same (300kg), they cancel out (and also the 2 dividing):

`v_(1i)^2+v_(2i)^2=v_(1f)^2+v_(2f)^2`

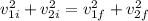
We then must solve this system:

`v_(1i)+v_(2i)=v_(1f)+v_(2f)`

`v_(1i)^2+v_(2i)^2=v_(1f)^2+v_(2f)^2`

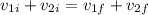
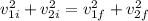
Which we will rewrite as:

`v_(1i)-v_(1f)=v_(2f)-v_(2i)`

`v_(1i)^2-v_(1f)^2=v_(2f)^2-v_(2i)^2`

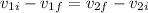
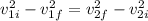
The last of these equations can be written as:

`(v_(1i)+v_(1f))(v_(1i)-v_(1f))=(v_(2f)+v_(2i))(v_(2f)-v_(2i))`

But we know that
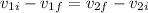`v_(1i)-v_(1f)=v_(2f)-v_(2i)`, so those cancel out:

`v_(1i)+v_(1f)=v_(2f)+v_(2i)`

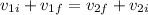
So we can write:

`v_(1i)-v_(1f)+v_(2i)=v_(2f)`

`v_(1i)+v_(1f)-v_(2i)=v_(2f)`

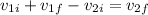
Which means:

`v_(1i)-v_(1f)+v_(2i)=v_(1i)+v_(1f)-v_(2i)`

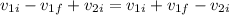
Which solving for the final velocity leaves us with:

`v_(2i)+v_(2i)=+v_(1f)+v_(1f)`

`v_(1f)=v_(2i)`

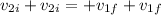
Grabbing any equation that relates both final velocities easily, for example
`v_(1i)-v_(1f)+v_(2i)=v_(2f)`, we obtain:

`v_(2f)=v_(1i)-v_(1f)+v_(2i)=v_(1i)-v_(1f)+v_(1f)=v_(1i)`

So we conclude that the bumpers have just exchanged velocities (something sometimes seen in billiards for example):

`v_(1f)=v_(2i)=5.9m/s`

`v_(2f)=v_(1i)=5.3m/s`