Question

The drawing shows a large cube (mass = 28.6 kg) being accelerated across a horizontal frictionless surface by a horizontal force P. A small cube (mass = 4.3 kg) is in contact with the front surface of the large cube and will slide downward unless P is sufficiently large. The coefficient of static friction between the cubes is 0.710. What is the smallest magnitude that P can have in order to keep the small cube from sliding downward?

Answer 1

P= 454.11 N

Step-by-step explanation:

Since P is the only horizontal force acting on the system, it can be defined as the product of the acceleration by the total mass of the system (both cubes).

`P= (M+m)*a\\a = (P)/(28.6 +4.3)\\a = (P)/(32.9)`

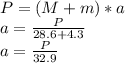
The friction force between both cubes (F) is defined as the normal force acting on the smaller cube multiplied by the coefficient of static friction. Since both cubes are subject to the same acceleration:

`F = m * a*\mu \\F= 4.3*0.710*(P)/(32.9)\\F=3.053*(P)/(32.9)`

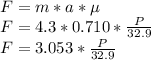
In order for the small cube to not slide down, the friction force must equal the weight of the small cube:

`3.053*(P)/(32.9) = 4.3 * g\\\\P = (4.3*9.8*32.9)/(3.053) \\P= 454.11 N`

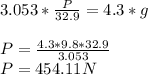
The smallest magnitude that P can have in order to keep the small cube from sliding downward is 454.11 N