Question

Given the domain(-4,0,5), what is the range for the relation 12x×6y=24?

Answer 1

The range has only two elements:

`-(1)/(12)`

`(1)/(15)`

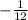
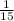
Explanation:

The range is the y set of number that are images of x. So, to find each range, we only need to replace each x value and find y.

`x = -4\\12x6y=24\\12(-4)6y= 24\\y=(24)/(-288)\\y = -(1)/(12)`

`x = 0\\12x6y=24\\y= (24)/(72x) \\y= (24)/(0)=\inf`

`x=5\\y= (24)/(72x)\\y= (24)/(72(5))=(24)/(260)=(1)/(15)`

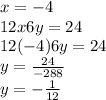
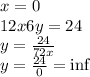
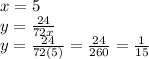
Therefore, the range of the given domain is
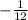`-(1)/(12)` and
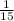`(1)/(15)`, the set has only two elements be cause x = 0 is undetermined, it doesn't have an image in y set.

Answer 2

The range is
`(-(1)/(12) ,(1)/(15))`. The realtion is no defined in 0.

Explanation:

Given the domain(-4,0,5)

For x=-4

12x×6y=24

12(-4)×6y=24

-48×6y=24

6y=
`(24)/(-48)`

y=
`(-1)/(2*6)`

y=
`(-1)/(12)`

For x=0

The relation is not defined

For x=5

12x×6y=24

12(5)×6y=24

60×6y=24

6y=
`(24)/(60)`

y=
`(2)/(5*6)`

y=
`(1)/(15)`