Answer:
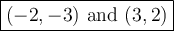
Explanation:
1. Solve the equations for x

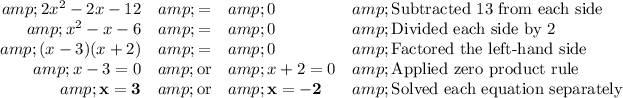
2. Calculate the corresponding values of y
Insert the values into equation (1)
(a) x = 3
y = 3 - 1 = 2
One point of intersection is (3, 2).
(b) x = -2
y = -2 - 1 = -3
The second point of intersection is (-2, -3).
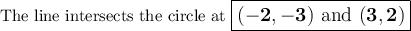
The diagram shows the intersection of the two graphs.