Answer:
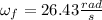
Step-by-step explanation:
Arc length of the circle is the measure of the distance between two points along the circumference, is given by:
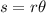
Solving for
 and replacing the given values:
and replacing the given values:
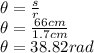
Now, we use a rotational kinematics formula in order to calculate the final angular velocity. Since the top is initially at rest
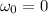 :
:
