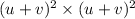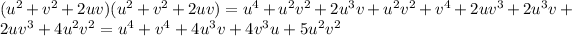Answer:
(a)
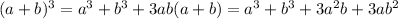
(b)
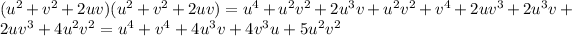
Explanation:
We have to expand the expression
(a)
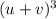 there are different methods for expanding the expression here u used algebraic identity for expansion
there are different methods for expanding the expression here u used algebraic identity for expansion
We know the algebraic identity
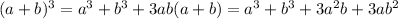
(b)
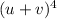
We know the algebraic identity
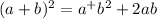
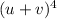 can be written as
can be written as