Answer:
Explanation:
To solve this problem, we must build the Venn's Diagram of these probabilities.
I am going to say that:
-The set A represents the probability that a family has a MasterCard.
-The set B represents the probability that a family has an American Express Card.
-The set C represents the probability that a family has a Visa card.
We have that
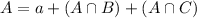
In which a represents the probability that the family only has a MasterCard,
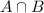 represents the probability that the family has both a MasterCard and an American Express card and
represents the probability that the family has both a MasterCard and an American Express card and
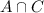 represents the probability that the family has both a Master and a Visa card.
represents the probability that the family has both a Master and a Visa card.
By the same logic, we also have that:
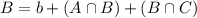
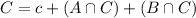
What is the probability of selecting a family that has either a Visa card or an American Express card?
This is
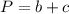 .
.
We start finding the probabilities from the intersection of these sets.
Six percent have both an American Express card and a Visa card. This means that:

Twelve percent have both a Visa card and a MasterCard

Eight percent of the families have both a MasterCard and an American Express card.
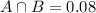
25% have a Visa card
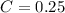
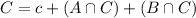
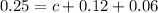
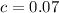
20% have an American Express card
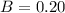
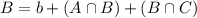
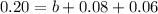
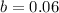
What is the probability of selecting a family that has either a Visa card or an American Express card?

There is a 13% probability of selecting a family that has either a Visa card or an American Express card