Question

Given f: ℝ → ℝ and : ℝ → ℝ , for the following, find f(g(x)) and g(f(x)), and state the domain.

a. f(x) = x2 − x, g(x) = x − 1
b. f(x) = x2 − x, g(x) = √x − 2
c. f(x) = x2, g(x) = 1 / x − 1
d. f(x) = 1 / x + 2, g(x) = 1 / x − 1
e. f(x) = x − 1, g(x) = log2(x + 3)

Answer 1

Remember,
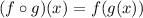`(f\circ g)(x)=f(g(x))` and the range of g must be in the domain of f.

a)

`f(g(x))=f(x-1)=(x-1)^2-(x-1)=x^2-2x+1-x+1=x^2-3x+2`

`g(f(x))=g(x^2-x)=(x^2-x)-1=x^2-x-1`

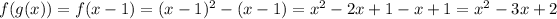
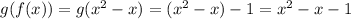
The domain of f(g(x)) and g(f(x)) is the set of reals.

b)

`f(g(x))=f(√(x)-2)=(√(x)-2)^2-x=√(x)^2-2*2*√(x)+2^2-x=-4√(x)+4`

`g(f(x))=g(x^2-x)=√(x^2-x)-2`

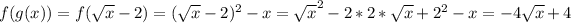
The domain of f(g(x)) is the set of nonnegative reals and the domain of g(f(x)) is the set of number such that
`x^2-x\geq 0`

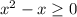
c)

`f(g(x))=f((1)/(x-1))=((1)/(x-1))^2=(1)/((x-1)^2)`

`g(f(x))=g(x^2)=(1)/(x^2-1)`

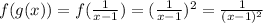
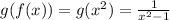
The domain of f(g(x)) is the set of reals except the 1 and the domain of g(f(x)) is the set of reals except the 1 and -1

d)

`f(g(x))=f((1)/(x-1))=(1)/(((1)/(x-1)-1))=(1)/((2-x)/(x-1))=(x-1)/(2-x)`

`g(f(x))=g((1)/(x+2))=(1)/(((1)/(x+2)-1))=(1)/((-x-1)/(x+2))=(x+2)/(-x-1)`

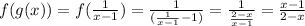
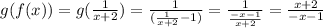
The domain of f(g(x)) is the set of reals except 2, and the domain of g(f(x)) is the set of reals except -1.

e)

`f(g(x))=f(log(2(x+3)))=f(log(2x+6))=log(2x+6)-1`

`g(f(x))=g(x-1)=log(2(x-1)+6)=log(2x+4)`

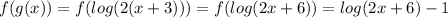
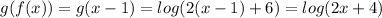
The domain of f(g(x)) is the set of nonnegative reals except -3. The domain of g(f(x)) is the set of nonnegative reals except -2.