Answer: The fourth set of sides
Explanation:
For a set of side lengths to form a right triangle, they have to satisfy the Pythagorean theory
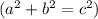
First set of sides
a = 7.5 b = 18 c = 21.5
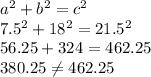
Second set of sides
a = 7.5 b = 19.5 c = 21.5
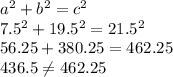
Third set of sides
a = 18 b = 19.25 c = 21.5
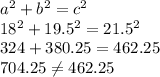
Fourth set of sides
a = 7.5 b = 18 c = 19.5
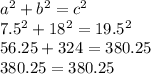
I hope that helped!