Step-by-step explanation:
The reaction equation will be as follows.
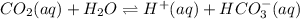
Calculate the amount of
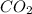 dissolved as follows.
dissolved as follows.

It is given that
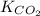 = 0.032 M/atm and
= 0.032 M/atm and
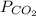 =
=
 atm.
atm.
Hence,
![[CO_(2)]](https://img.qammunity.org/2020/formulas/chemistry/college/kbfvn81a84l7bcz4ysd6tqnt34djkqcfkv.png) will be calculated as follows.
will be calculated as follows.
![[CO_(2)]](https://img.qammunity.org/2020/formulas/chemistry/college/kbfvn81a84l7bcz4ysd6tqnt34djkqcfkv.png) =
=
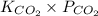
=
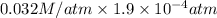
=
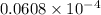
or, =
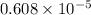
It is given that
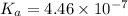
As,
![K_(a) = ([H^(+)]^(2))/([CO_(2)])](https://img.qammunity.org/2020/formulas/chemistry/college/30h27wdsy07ecxbxigmjhtnmvnyovroh4p.png)
![4.46 * 10^(-7) = ([H^(+)]^(2))/(0.608 * 10^(-5))](https://img.qammunity.org/2020/formulas/chemistry/college/qfd675sf6td4jwthnozuq7j9tulb66a4rj.png)
![[H^(+)]^(2)](https://img.qammunity.org/2020/formulas/chemistry/college/1c9nwtzgmcm38kw65vp6uj4qnqharsay8u.png) =
=
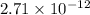
![[H^(+)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/axnvi9gez4h3rovfp1qidd16ya8d7gzbon.png) =
=
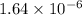
Since, we know that pH =
![-log [H^(+)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/gopcqwordys161r0cdra5oyonsnub5hpxq.png)
So, pH =
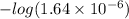
= 5.7
Therefore, we can conclude that pH of water in equilibrium with the atmosphere is 5.7.