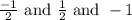Question

Solve the equation 4x^3 + 4x^2-x-1 = 0 given that -1/2 is a zero of f(x) = 4x^3 + 4x^2-x-1.

Answer 1

The solution of equation 4x^3 + 4x^2-x-1 = 0 given that -1/2 is a zero of f(x) = 4x^3 + 4x^2-x-1 is
`(-1)/(2) \text { and } (1)/(2) \text { and }-1`

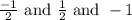
Solution:

Given, cubic equation
`4 x^(3)+4 x^(2)-x-1=0`

And
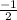`(-1)/(2)` is a zero of
`f(x)=4 x^(3)+4 x^(2)-x-1`

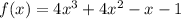
We have to find the other two roots of the given quadratic equation.

Let the other two roots be a, b.

Now, we know that, sum of roots of cubic equation
`=\frac{-x^(2) \text { coefficient }}{x^(3) \text { coefficient }}`

`\text { Then, } (-1)/(2)+a+b=(-4)/(4) \rightarrow a+b=-1+(1)/(2) \rightarrow a+b=(-1)/(2) \rightarrow(1)`

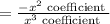
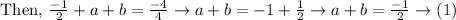
Now, product of roots of cubic equation
`=\frac{-\text { constant value }}{x^(3) \text { coefficient }}`

`\begin{array}{l}{\text { Then, } (-1)/(2) * a * b=(-(-1))/(4) \rightarrow (-1)/(2) * a b=(1)/(4)} \\\\ {\rightarrow a b=-2 * (1)/(4) \rightarrow a b=(-1)/(2)}\end{array}`

`\text { Now we know that, }(a-b)^(2)=(a+b)^(2)-4 a b`

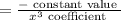
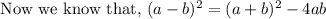
substitute above value in this formula

`(a-b)^(2)=\left((-1)/(2)\right)^(2)-4 *\left((-1)/(2)\right)`

`(a-b)^(2)=1 / 4+2 \rightarrow(a-b)^(2)=(2 * 4+1)/(4) \rightarrow(a-b)^(2)=(9)/(4) \rightarrow a-b=(3)/(2) \rightarrow(2)`

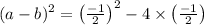
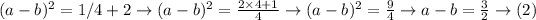
Now, solve (1) and (2)

`\begin{array}{l}{2 a=(3-1)/(2)} \\ {2 a=1} \\ {a=(1)/(2)}\end{array}`

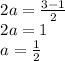
substitute "a" value in (1)

`(1)/(2)+b= (-1)/(2) \rightarrow b= (-1)/(2) + (-1)/(2) \rightarrow b=-1`

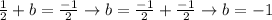
Hence, the roots of the given cubic equation are
`(-1)/(2) \text { and } (1)/(2) \text { and }-1`