Question

Let m(x) = x / x−1

a. Find the inverse of m.
b. Graph m. How does the graph of m explain why this function is its own inverse?
c. Think of another function that is its own inverse.

Answer 1

Answer with Step-by-step explanation:

We are given that a function

`m(x)=(x)/(x-1)`

a.We have to find the inverse of m.

Suppose,
`y=m(x)=(x)/(x-1)`

`yx-y=x`

`yx-x=y`

`x(y-1)=y`

`x=(y)/(y-1)`

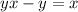
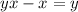
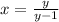
Replace x by y and y by x

`y=(x)/(x-1)`

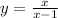
Substitute
`y=m^(-1)(x)`

`g(x)=m^(-1)(x)=(x)/(x-1)`

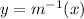
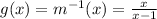
b.When the inverse function of given function is
`(x)/(x-1)`

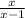
Then , we get fog(x)=
`f(g(x))=((x)/(x-1))/((x)/(x-1)-1)`

`fog(x)=(x)/(x-x+1)=x=I(x)`

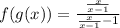
When f and g are inverse to each other then fog(x)=Identity function.

c.If f(x)=x

It is self inverse function.