Answer:
(a) Factor will be (x-1)
 x = 1 , -1+2i and -1-2i
x = 1 , -1+2i and -1-2i
(b) Solution of the equation will be
Explanation:
We have given that 1 is the zero of the polynomial
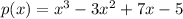
(a) As x is zero of the polynomial so (x-1) will completely divide the polynomial
So
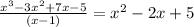
Now
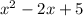 can be factorized as
can be factorized as

So the linear factor of polynomial
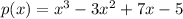 will be
will be
(x-1)

(b) Solution of the equation will be x = 1 , -1+2i and -1-2i