Question

If x-9 is a factor of x2 – 5x – 36, what is the other factor?

X-4
X+4
X-6
X+6

Answer 1

the right answer was suppose to be -9, because it says (x-9) , so wherever you see x you multiple it by the number giving

Explanation:

(-9)2-5(-9)=-18+45-36

Answer 2

(x + 4)

Explanation:

The given expression is

`x^(2) -5x-36`

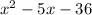
To its factor, we can use the quadratic formula

`x_(1,2)=\frac{-b (+-)\sqrt{b^(2)-4ac } }{2a}`

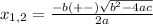
Where

`a=1\\b=-5\\c=-36`

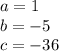
Replacing these values in the quadratic formula, we have

`x_(1,2)=\frac{-(-5) (+-)\sqrt{(-5)^(2)-4(1)(-36) } }{2(1)}=(5(+-)√(25+144) )/(2) =(5(+-)√(169) )/(2)=(5(+-)13)/(2)\\x_(1)=(5+13)/(2)=(18)/(2)=9\\x_(2)=(5-13)/(2)=(-8)/(2)=-4`

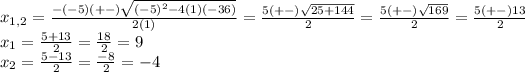
As you can observe the two factors must be
`(x-9)(x+4)=0`

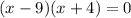
Therefore, the right answer is the second choice, (x + 4) is the other factor of the quadratic expression.