Question

PLEASE HELP!!! What is m∠AEB?

Enter your answer in the box.


°



Line B D is slightly inclined with vertical intersects with line A C at E. Point C is on right side of line B D. The left upward and right downward angles of the intersecting lines are obtuse. The measure of angle A E B is labeled as left parenthesis 5 x minus 10 right parenthesis degrees. The measure of angle C E D is labeled as left parenthesis 3 x plus 40 right parenthesis degrees.

Answer 1

m/_AEB = 115 degrees

Explanation:

Hope this helps! :)

Answer 2

m∠AEB=115°

Explanation:

we know that

Vertical Angles are the angles opposite each other when two lines cross. Vertical angles are always congruent.

In this problem

m∠AEB=m∠CED -----> by vertical angles

substitute the values

`(5x-10)\°=(3x+40)\°`

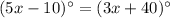
Solve for x

`5x-3x=40+10`

`2x=50`

`x=25`

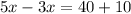
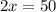
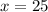
Find out the measure of m∠AEB

m∠AEB=(5x-10)°

substitute the value of x

m∠AEB=(5(25)-10)=115°