Question

Miller Corporation has a premium bond making semiannual payments. The bond pays a coupon of 10 percent, has a YTM of 8 percent, and has 14 years to maturity. The Modigliani Company has a discount bond making semiannual payments. This bond pays a coupon of 8 percent, has a YTM of 10 percent, and also has 14 years to maturity.What is the price of each bond today? Price of Miller Corporation bond $ ____ Price of Modigliani Company bond $ ____If interest rates remain unchanged, what do you expect the prices of these bonds to be 1 year from now? In 4 years? In 9 years? In 13 years? In 14 years? (Do not round intermediate calculations and round your answers to 2 decimal places, e.g., 32.16.)Price of bond Miller Corporation Bond Modigliani Company Bond 1 year $ _________ $ _________ 4 years $ _________ $_________ 9 years $ _________ $_________ 13 years $ _________ $ _________ 14 years $_________ $_________

Answer 1

The prices of the Miller Corporation bond and Modigliani Company bond can be calculated by discounting their future cash flows at their respective YTMs. These calculations account for semiannual payments and prevailing interest rates. Over time, and assuming unchanged interest rates, bond prices will change reflecting their diminishing time to maturity.

Step-by-step explanation:

To calculate the price of the Miller Corporation bond and the Modigliani Company bond, we must discount the future cash flows of each bond to their present values using their respective yields to maturity (YTM). Since both bonds make semiannual payments, this needs to be considered in the calculation by adjusting the rates and periods.

The Miller Corporation bond has a coupon rate of 10% and a YTM of 8%, while the Modigliani Company bond has a coupon rate of 8% and a YTM of 10%. Both have 14 years to maturity. We also have to take into account the face value of the bonds, which is typically $1,000 unless stated otherwise.

By applying the present value formula to the coupon payments and face value, we can find the current price of each bond. However, since the bonds' exact face values are not provided, we will use an assumed face value of $1,000 for demonstration purposes. If interest rates remain unchanged, the price of the bonds one year, four years, nine years, and thirteen years from now would be calculated using similar discounting of the remaining cash flows. At maturity (14 years), the price of both bonds would converge to their face value.

For the discount bond (Modigliani Company), as it approaches maturity, its price will increase towards the face value assuming the YTM remains the same.

Answer 2

Miller Bond:

Today: 1,166.63

1-year 1,159.83

4-years 1,135.90

9-years 1,081.11

13-years 1,018.86

14-years 1,000 (maturity)

Modigliani Bond

Today: 851.01

1-year 856.25

4-years 875.38

9-years 922.78

13-years 981.41

14-years 1,000 (maturity)

Step-by-step explanation:

The present value will be the discount coupon payment and maturirty at the YTM rate:

Miller Bond:

The coupon payment are calcualte as ordinary annuity

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 50.00 (1,000 x 10% / 2)

time 28 (14 years x 2 payment per year)

rate 0.04 (8% YTM / 2 payment per year)

`50 * (1-(1+0.04)^(-28) )/(0.04) = PV\\`

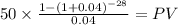
PV $833.1532

While Maturity, using the lump sum formula

`(Maturity)/((1 + rate)^(time) ) = PV`

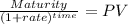
Maturity $1,000.00

time 28 semesters

rate 0.04

`(1000)/((1 + 0.04)^(28) ) = PV`

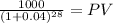
PV 333.48

PV coupon $833.1532 +PV maturity $333.4775 = Total $1,166.6306

For the subsequent time we must adjust t

in one year, there will be 26 payment until maturity

`50 * (1-(1+0.04)^(-26) )/(0.04) = PV\\`

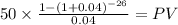
PVcoupon $799.1385

`(1000)/((1 + 0.04)^(26) ) = PV`

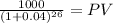
PVmaturity 360.69

Total $1,159.8277

As the bond get closer to maturity it will get closer to face value until maturity when it will equalize it.

We recalculate the same formula with values of:

in 4-year : then 10 years to maturity t = 20

in 9-years: then 5 years to maturity t= 10

in 13-years: 1 year to maturity t = 2

at 14 years: is maturity date so equals the face value of 1,000

Remember: there are two payment per year.

Same process will be done with Modigliani bond:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 1,000 x 8% / 2 payment per year : 40.00

time: 14 years x 2 payment per year = 28 payment

rate 10% annual rate /2 = 0.05

`40 * (1-(1+0.05)^(-28) )/(0.05) = PV\\`

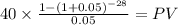
PV coupon $595.9251

`(Maturity)/((1 + rate)^(time) ) = PV`

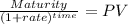
Maturity $ 1,000.00

time 28 semester

rate 0.05

`(1000)/((1 + 0.05)^(28) ) = PV`

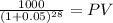
PV maturity 255.09

PV coupon $595.9251 + PV maturity $255.0936 = Total $851.0187

and then we calcualte for the same values of t we are asked for the Miller bond.