Question

On a coordinate plane, a dashed straight line has a positive slope and goes through (negative 4, 0) and (0, 2). Everything below the line is shaded.

Which points are solutions to the linear inequality y < 0.5x + 2? Select three options.



(–3, –2)

(–2, 1)

(–1, –2)

(–1, 2)

(1, –2)

Answer 1

(–3, –2), (–1, –2) and (1, –2)

Explanation:

The given inequality is

`y<0.5x+2`

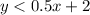
We need to check which points are solutions to the linear inequality y < 0.5x + 2.

Check the inequality be each given point.

For (-3,-2),

`-2<0.5(-3)+2`

`-2<-1.5+2`

`-2<0.5`

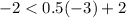
The statement is true. It means (-3,2) is a solution of given inequality.

Similarly,

For (-2,1),

`1<0.5(-2)+2`

`1<1`

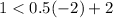
The statement is false. It means (-2,1) is not a solution of given inequality.

For (-1,-2),

`-2<0.5(-1)+2`

`-2<1.5`

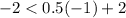
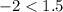
The statement is true. It means (-1,-2) is a solution of given inequality.

For (-1,2),

`2<0.5(-1)+2`

`2<1.5`

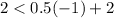
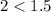
The statement is false. It means (-1,2) is not a solution of given inequality.

For (1,-2),

`-2<0.5(1)+2`

`-2<2.5`

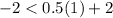
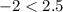
The statement is true. It means (1,-2) is a solution of given inequality.

Answer 2

(-3,-2), (-1,-2), (1,-2)

Explanation:

Each point on the plane is of the form (x,y). let's see which points satisfy the inequality
`0.5x+2>y`

a)

`0.5(-3)+2=-1.5+2=0.5>-2`, then (-3,-2) satisfies the inequality.

b)

`0.5(-2)+2=-1+2=1`, then (-2,1) doesn't satisfy the inequality

c)

`0.5(-1)+2=-0.5+2=1.5>-2`, then (-1,-2) satisfies the inequality.

d)

`0.5(-1)+2=1.5<2`, then (-1,2) doesn't satisfy the inequality.

e)

`0.5(1)+2=0.5+2=2.5>-2`, then (1,-2) satisfies the inequality.