Answer:
x² + 2y² = 2
Explanation:
The general form of a complex number z in the Cartesian coordinate plane is given by z = x + iy ........ (1)
Now, the given complex number is z = √2 CosФ + i SinФ ....... (2)
Hence, comparing equations (1) and (2), we get, x = √2 CosФ and y = SinФ
Now, we can eliminate Ф to combine the above two equations as
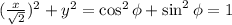
⇒ x² + 2y² = 2.
Therefore, this is the algebraic equation required, which is the path traced by the given complex number z. (Answer)