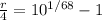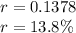Answer:
r=13.8%
Explanation:
we know that
The compound interest formula is equal to
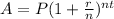
where
A is the Final Investment Value
P is the Principal amount of money to be invested
r is the rate of interest in decimal
t is Number of Time Periods
n is the number of times interest is compounded per year
in this problem we have
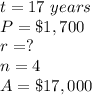
substitute in the formula above
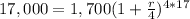
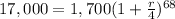
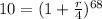
Elevate both sides to 1/68