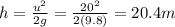Question

a ball is thrown vertically upward with a velocity of 20m/s. what is the maximum height after 30secs​

Answer 1

Maximum height: 20.4 m, height at 30 s: -274 m

Step-by-step explanation:

If you want to find the height of the ball after 30 seconds, we must use the equation:

`v=u+at`

where

u = 20 m/s is the initial velocity

a = g = -9.8 m/s^2 is the acceleration of gravity

t is the time

Substituting t = 30 s,

`v=20+(-9.8)(30)=-274 m`

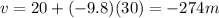
This means that the ball is 274 m below its original level.

If you want to find the maximum height, then it can be find by using the law of conservation of energy: in fact, at the maximum height, all the initial kinetic energy has been converted into potential energy, so

`mgh = (1)/(2)mu^2`

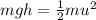
And solving for h, we find the maximum height:

`h=(u^2)/(2g)=(20^2)/(2(9.8))=20.4 m`