Question

An airplane can fly 650 miles per hour in still air. If it can travel 2800 miles with the wind in the same it can travel 2400 miles against the wind, find the wind speed.

Answer 1

The speed of the wind is 8450 miles.

Solution:

Given, An airplane can fly 650 miles per hour in still air.

It can travel 2800 miles with the wind in the same time it can travel 2400 miles against the wind,

We have to find the wind speed.

Let the speed of the wind be s.

Now, we know that, distance travelled = relative speed x time taken.

While travelling with wind

`\rightarrow 2800=(s+650) * \text { time taken } \rightarrow \text { time taken }=(2800)/(s+650)`

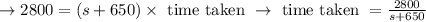
[s + 650 is relative speed as both are in same direction]

While travelling against wind

`\rightarrow 2400=(s-650) * \text { time taken } \rightarrow \text { time taken }=(2400)/(s-650)`

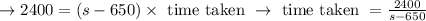
Here, both time taken are equal as given that same time.

Now, equate both equations

`\begin{array}{l}{\rightarrow (2800)/(s+650)=(2400)/(s-650)} \\\\ {28 *(s-650)=24 *(s+650)} \\\\ {28 s-28 * 650=24 s+24 * 650} \\\\ {28 s-24 s=24 * 650+28 * 650} \\\\ {4 s=(24+28) * 650}\end{array}`

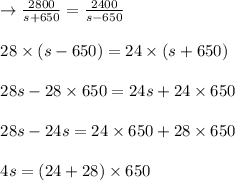
4s = 52 x 650 = 13 x 650 = 8450

Hence, the speed of the wind is 8450 miles.