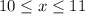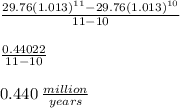Question

The population of California was 29.76 million in 1990 and 33.87 million in 2000. Use the model found in part a (f(x) =29.76(1.013)^t to find the average rate of change from 1990 to 1991 and from 2000 to 2001. (Round your answer to the nearest thousand.)

Answer 1

The average rate of change from 1990 to 1991 is
`0.387 \:(million)/(years)`

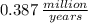
The average rate of change from 2000 to 2001 is
`0.440 \:(million)/(years)`

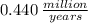
Explanation:

The average rate of change of function f(x) over the interval
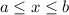`a\leq x\leq b` is given by

`(f(b)-f(a))/(b-a)`

It is a measure of how much the function changed per unit, on average, over that interval.

From the information given:

• The function that models the population t years after 1990 is
  `f(t) =29.76(1.013)^t`
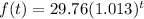
• The year 1990 is t = 0 and the year 2000 is t = 10.

1. The average rate of change from 1990 to 1991 is:

The interval is
`0\leq x\leq 1`

`(29.76(1.013)^1-29.76(1.013)^0)/(1-0)\\\\(1.013^1\cdot \:29.76-1\cdot \:29.76)/(1-0)\\\\(0.38688)/(1-0)\\\\0.387 \:(million)/(years)`

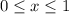
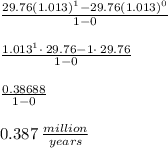
2. The average rate of change from 2000 to 2001 is

The interval is
`10\leq x\leq 11`

`(29.76(1.013)^(11)-29.76(1.013)^(10))/(11-10)\\\\(0.44022)/(11-10)\\\\0.440 \:(million)/(years)`