Question

The drawing shows identical stones that are being whirled on a tabletop at the same speed. The radius of the larger circle is twice that of the smaller circle. How is the tension t1 in the longer cord related to the tension t2 in the shorter cord?

Answer 1

`T_1=(T_2)/(2)`

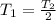
Step-by-step explanation:

The drawing is missing but we can still answer.

In fact, for a stone being whirled on a tabletop, the tension in the cord provides the centripetal force that keeps the stone in circular motion; therefore we can write:

`T=m(v^2)/(r)`

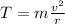
where

T is the tension

m is the mass of the stone

v is the speed

r is the radius of the circle

For the first stone, we have

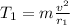`T_1=m(v^2)/(r_1)` (1)

While for the second stone,

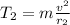`T_2=m(v^2)/(r_2)` (2)

since m and v are identical for the two stones. We know that the first cord is longer, such that the radius of the circle in the 1st case is twice that of the second case:

`r_1 = 2 r_2`

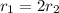
So, substituting into (1),

`T_1=m(v^2)/(2 r_2)=(T_2)/(2)`

which means that the tension in the longer cord is half the tension in the shorter cord.