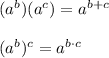Answer:
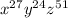
Explanation:

_____
You can recognize that the denominator factor is also one of the numerator factors, so can be cancelled right away. Proceeding to evaluate inside parentheses first, we get ...
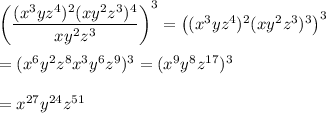
_____
The rules of exponents that apply are ...