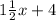Question

The expression 3 1/2x + 18 represents the perimeter of the rectangle shown. Write an expression that represents the length of the rectangle.

A. 3 1/4x + 13
B. 1 1/2x + 8
C. 3x + 8
D. 1 1/2x + 4

Answer 1

D)

Explanation:

3 1/2=7/2

2(1/4x+5)+2y=7/2x+18

2/4x+10+2y=7/2x+18

1/2x+10+2y=7/2x+18

2y=7/2x+18-1/2x-10

2y=6/2x+18-10

2y=3x+8

y=3/2x+8/2

y=3/2x+4

Answer 2

D) The Length of the rectangle is
`1(1)/(2)x  + 4`

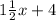
Explanation:

Here, the width of the rectangle =
`(1)/(4)x + 5`

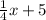
Let the length of the rectangle = L

Also, given the perimeter of the figure =
`3( (1)/(2)) x + 18`

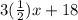
Now we know that, Perimeter of the Rectangle = 2(Length + Width)

or,
`3( (1)/(2)) x + 18 = 2(L + (1)/(4)x + 5)`

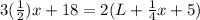
Solving for L, we get :

`2L + (x)/(2) + 10 = (3x)/(2)  +18\\ or, 2L = (3x)/(2)  - (x)/(2)   + 18 -10\\or, L = (2x)/(2)  + (8)/(2)`

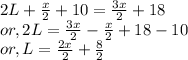
Hence the length of the rectangle is , D)
`1(1)/(2)x  + 4`