Question

Solve 3x + 2 = 15 for x using the change of base formula log base b of y equals log y over log b. −1.594 0.465 2.406 4.465

Helppppppp - time is of the essence!!!!

Answer 1

0.465

Explanation:

Solve 3x + 2 = 15 for x using the change of base formula log base b of y equals log y over log b. −1.594 0.465 2.406 4.465

rearranging the question

`3^(x+2) =15`.........1

the change of base in logarithm is given by.

`log_(b) a=(loga)/(logb)`

back to equation 1

taking logarithm of the other end

x+2=
`log_(3) 15`

x+2=log 15/log 3

also

we could write

x+2(log3)=log15

x+2=2.465

x=2.465-2

x=0.465

Answer 2

The value in 3x + 2 = 15 for x using the change of base formula is 0.465 approximately and second option is correct one.

Solution:

Given, expression is
`3^((x+2))=15`

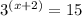
We have to solve the above expression using change of base formula which is given as

`\log _(b) a=(\log a)/(\log b)`

Now, let us first apply logarithm for the given expression.

Then given expression turns into as,
`x+2=\log _(3) 15`

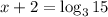
By using change of base formula,

`x+2=(\log _(10) 15)/(\log _(10) 3)`

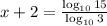
x + 2 = 2.4649

x = 2.4649 – 2 = 0.4649

Hence, the value of x is 0.465 approximately and second option is correct one.