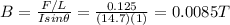Question

A conductor carrying 14.7 amps of current is directed along the positive x-axis and perpendicular to a uniform magnetic field. A magnetic force per unit length of 0.125 n/m acts on the conductor in the negative y direction. What is the strength of the magnetic field at the place where the current is?

Answer 1

0.0085 T

Step-by-step explanation:

The magnetic force per unit length exerted on a current-carrying wire is given by

`(F)/(L)=BI sin \theta`

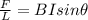
where

B is the strength of the magnetic field

I is the current

`\theta` is the angle between the directions of B and I

In this problem, we know

`(F)/(L)=0.125 N/m`

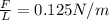
I = 14.7 A (the current)

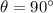`\theta=90^(\circ)` since I and B are perpendicular

Therefore, solving for B, we find the strength of the field:

`B=(F/L)/(I sin \theta)=(0.125)/((14.7)(1))=0.0085 T`