Question

Slope = 2 passing through (6,2)

Answer 1

The equation of slope = 2 passing through (6, 2) is y = 2x - 12

Solution:

Given that, slope = 2 and a point is (6, 2)

We have to find the line that passes through the (6, 2) and having slope 2.

Now we know that,

Point – slope form of a line is

`y-y_(1)=m\left(x-x_(1)\right) \text { where }\left(x_(1), y_(1)\right) \text { is a point on line and } m \text { is slope of line. }`

`\text { In our problem, } m=2, x_(1)=6, y_(1)=2`

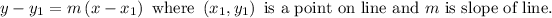
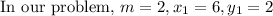
Substitute these values in point – slope form.

y – 2 = 2(x – 6)

y – 2 = 2x – 12

2x – y = 12 – 2

2x – y = 10

hence, the line equation is y = 2x - 12