Answer:
The factorization of given expression
 is (x + 9i)(x – 9i) and option d is correct.
is (x + 9i)(x – 9i) and option d is correct.
Solution:
Given, expression is

We have to factor it in the complex numbers.
Let us check options to find answer.
A) (x – 9)(x – 9)
(x – 9)( x – 9)
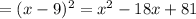
So, this is not correct answer.
B) (x + 9)(x + 9)

So, this is not correct answer.
C) (x + 9i)(x + 9i)
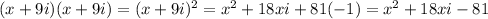
So, this is not correct answer.
D) (x + 9i)(x - 9i)
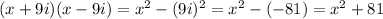
Thus option D is correct
Hence, the factorization of given expression is (x + 9i)(x – 9i). and option d is correct.