Question

1. Write the exponential function f(x) = -4^(x-2) in the form f(x) = ab^x​

Answer 1

`\displaystyle f(x)=-(1)/(16)(4^x)`

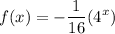
Explanation:

We have the function:

`f(x)=-4^(x-2)`

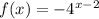
And we want to convert this to the exponential form:

`f(x)=ab^x`

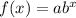
First, using the power of a product property, we can rewrite our function as:

`f(x)=-(4^x\cdot4^(-2))`

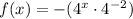
By evaluating the second term, we acquire:

`\displaystyle f(x)=-\big(4^x\cdot (1)/(4)^2}\big)=-\big(4^x\cdot (1)/(16)\big)`

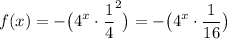
So, by rearranging, we acquire:

`\displaystyle f(x)=-(1)/(16)(4^x)`

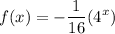
As desired.