Question

A music industry researcher wants to estimate, with a 90% confidence level, the proportion of young urban people (ages 21 to 35 years) who go to at least 3 concerts a year. Previous studies show that 35% of those people (21 to 35 year olds) interviewed go to at least 3 concerts a year. The researcher wants to be accurate within 2% of the true proportion. Find the minimum sample size necessary.

Choose one • 10 points

2185

1539

2401

8740

Answer 1

1,539

Explanation:

Using Simple Random Sampling in an infinite population (this is such a large population that we do not know the exact number) we have that the sample size should be the nearest integer to

`\large (Z^2pq)/(e^2)`

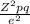
where

Z= the z-score corresponding to the confidence level, in this case 90%, so Z=1.645 (this means that the area under the Normal N(0,1) between [-1.645,1.645] is 90%=0.9)

p= the proportion of young urban people (ages 21 to 35 years) who go to at least 3 concerts a year= 35% = 0.35

q = 1-p = 0.65

e = the error proportion = 2% = 0.02

Making the calculations

`\large (Z^2pq)/(e^2)=((1.645)^2*0.35*0.65)/((0.02)^2)=1,539.09`

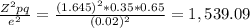
So, the sample size should be 1,539 young urban people (ages 21 to 35 years)