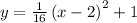Question

The x- and y-coordinates of the focus of a parabola are (1,3) and the directrix is y=-5 . A second parabola is a translation 1 unit right and 2 units up of the first parabola. Write an equation of the second parabola.

Answer 1

The equation of the second parabola is
`y=(1)/(16) \left(x - 2\right)^(2) + 1`

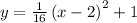
Explanation:

We know that the focus of the first parabola is (1,3) and the directrix is y = -5. We also know that the second parabola is a translation 1 unit right and 2 units up of the first parabola.

We can use the focus of the first parabola to find the focus of the second parabola (1+1, 3+2) = (2, 5) and the directrix of the second parabola is moved 2 units up. The equation of the directrix of the second parabola is y = -3.

To find the parabola equation we start by assuming a general point on the parabola (x,y).

Next, with the help of the distance formula we find that the distance between (x,y) and the focus.

`√((x-2)^2+(y-5)^2)`

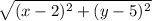
The distance between (x,y) and the directrix y = -3 is
`√((y+3)^2)`

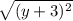
On the parabola, these distances are equal:

`√(\left(y+3\right)^2)=√(\left(x-2\right)^2+\left(y-5\right)^2)\\\left(√(\left(y+3\right)^2)\right)^2=\left(√(\left(x-2\right)^2+\left(y-5\right)^2)\right)^2\\\\\left(y+3\right)^2=\left(x-2\right)^2+\left(y-5\right)^2\\\\\left(y+3\right)^2= x^2-4x+4+y^2-10y+25\\\left(y+3\right)^2=x^2-4x+y^2+29-10y\\\\y^2+6y+9=x^2-4x+y^2+29-10y\\16y=x^2-4x+20\\y=(x^2-4x+20)/(16)\\\\y=(1)/(16) \left(x - 2\right)^(2) + 1`

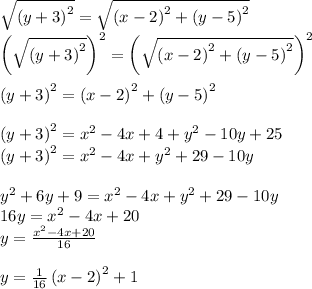
The equation of the second parabola is
`y=(1)/(16) \left(x - 2\right)^(2) + 1`