Answer:
1 and −1 are the only solutions to the equation x^2 = 1.
Explanation:
We shall proceed as he suggests
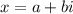
Given
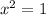
substitute a+bi in x, we get
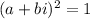
Rewriting the both sides in standard form for a complex number
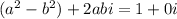
Equating the real parts on each side of the equation, and equating the imaginary parts on each side of the equation.
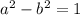 and
and

So either a=0 or b=0. If a=0 then

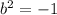 . has no real solution.
. has no real solution.
If b=0 then
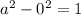
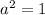
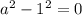
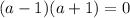
 . or
. or

Hence proved.