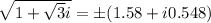Question

Use the method in the Example to find the square roots of 1 + √3i

Answer 1

`\sqrt{1 + √(3) i}=\pm (1.58+i 0.548)`

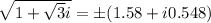
Explanation:

Given

z = 1 + √3 i

Let
`√(1+\sqrt(3) i)=p+iq`

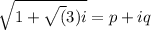
Squaring both sides

`1+\sqrt(3) i=p^2-q^2+2ipq`

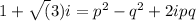
Comparing real and imaginary part

Re(LHS)=Re(RHS)

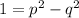`1=p^2-q^2`...........................(1)

comparing Im(LHS)=Im(RHS)

√3=2pq

`q=(√(3))/(2p)`

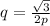
Substitute q in equation (1)

`1=p^2-((√(3))/(2p))^2`

`p^4-p^2-0.75=0`

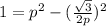
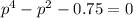
Let
`x=p^2`

`x^2-x-0.75=0`

`x=(1\pm √(1^2+4* 0.75))/(2)`

`x=(1\pm 4)/(2)`

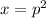
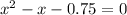
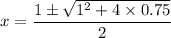
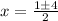
we take only Positive value because
`p^2=x`

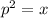
x=2.5

`p^2=2.5`

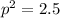
thus
`p=\pm 1.58`

`q=\pm 0.548`

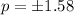
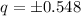
thus,

`\sqrt{1 + √(3) i}=\pm (1.58+i 0.548)`