Question

The following procedure provides a crude method of determining the molar mass of a volatile liquid. A liquid of mass 0.0224 g is introduced into a syringe and the end is capped (sealed). The syringe is transferred to a temperature bath maintained at 49.9 oC, and the liquid vaporizes. As the liquid vaporizes the plunger is pushed out. At equilibrium, the plunger reads 6.56 mL of gas. Atmospheric pressure is 740. mmHg. What is the approximate molar mass of the compound (in g/mol)?

Answer 1

Step-by-step explanation:

We know that 740 mm Hg = 0.97368 atm

According to ideal behavior for the vapor,

PV = nRT

here, R = 0.082 L
`atm mol^(-1)K^(-1)`

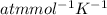
T = 273.15 + 62.7 = 335.85 K

V =
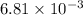`6.81 * 10^(-3)` L

Therefore, first we will calculate the number of moles as follows.

n =
`(PV)/(RT)`

=
`(0.97368 * 6.56 * 10^(-3))/(0.082 * 322.9)`

=
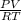
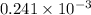`0.241 * 10^(-3)` moles

Now, molar mass of the given compound will be calculated as follows.

Number of moles =
`\frac{mass}{\text{molar mass}}`

`0.241 * 10^(-3) mol = \frac{0.0224 g}{\text{molar mass}}`

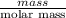
molar mass = 92.94 g/mol

Thus, we can conclude that molar mass of the compound is 92.94 g/mol.

Answer 2

78.85 g/mol

Step-by-step explanation:

The molecular weight can easily be calculated from the ideal gas law if we have all the information since:

PV = nRT but n= m/MW

therefore substituting and rearranging the equation we have

PV= (m/MW) RT

MW= mRT/(PW)

attached please find the calculation