Question

Triangle R Q S is cut by line segment T V. Line segment T V goes from side Q R to side R S. The length of R V is x + 10, the length of V S is x, the length of R T is x + 4, and the length of T Q is x minus 3.

Which value of x would make Line segment T V is parallel to Line segment Q S?



3


8


10


11

Answer 1

C.

Explanation:

Lovely.

Answer 2

Option C.

Explanation:

Given information: TV║QS, RV=x+10, VS=x, RT=x+4 and TQ=x-3.

Triangle Proportionality Theorem: This theorem states that if a line segment is parallel to the base of a triangle and it intersects the other two sides, then it divides those sides proportionally.

Using the Triangle Proportionality Theorem, we get

`(RT)/(TQ)=(RV)/(VS)`

Substitute the given values in the above equation.

`(x+4)/(x-3)=(x+10)/(x)`

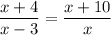
On cross multiplication we get

`x(x+4)=(x+10)(x-3)`

`x^2+4x=x^2-3x+10x-30`

`x^2+4x=x^2+7x-30`

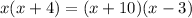
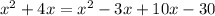
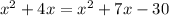
Subtract x² from both sides.

`x^2+4x-x^2=x^2+7x-30-x^2`

`4x=7x-30`

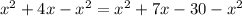
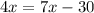
Subtract 7x from both sides.

`4x-7x=7x-30-7x`

`-3x=-30`

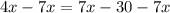
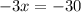
Divide both sides by -3.

`x=(-30)/(-3)`

`x=10`

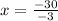
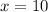
The value of x is 10. Therefore, the correct option is C.