Question

In most of its ionic compounds, cobalt is either Co(II) or Co(III). One such compound, containing chloride ion and waters of hydration, was analyzed, and the following results were obtained. A 0.256-g sample of the compound was dissolved in water, and excess silver nitrate was added. The silver chloride was filtered, dried, and weighed, and it had a mass of 0.308 g. A second sample of 0.416 g of the compound was dissolved in water, and an excess of sodium hydroxide was added. The hydroxide salt was filtered and heated in a flame, forming cobalt(III) oxide. The mass of the cobalt(III) oxide formed was 0.145 g. What is the percent composition, by mass, of the compound?

Answer 1

Answer: The mass percent of
`Co^(3+),Cl^(-),H^+\text{ and }O^(2-)` ions in the compound are 49.28 %, 29.79 %, 2.33 % and 18.63 % respectively

Step-by-step explanation:

We are given:

Mass of silver chloride = 0.308 grams

Mass of cobalt (III) oxide = 0.145 grams

Mass of sample containing chloride ions = 0.256 grams

Mass of sample containing
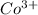`Co^(3+)` ions = 0.416 grams

We know that:

Molar mass of silver chloride = 143.4 g/mol

Molar mass of chlorine ion = 35.45 g/mol

Molar mass of cobalt (III) oxide = 165.86 g/mol

Molar mass of
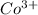`Co^(3+)` ion = 117.86 g/mol

Molar mass of water = 18 g/mol

Molar mass of hydrogen ion = 1 g/mol

Molar mass of oxygen ion = 16 g/mol

To calculate the number of moles, we use the equation:

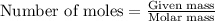`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}` ......(1)

To calculate the mass percentage of ions in sample, we use the equation:

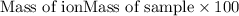`\text{Mass of ion}}{\text{Mass of sample}}* 100` .......(2)

• For chlorine ion:

Calculating moles of AgCl by using equation 1:

Moles of AgCl =
`(0.308g)/(143.4g/mol)=0.00215mol`

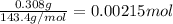
The chemical equation for the ionization of silver chloride follows:

`AgCl\rightarrow Ag^++Cl^-`

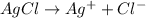
By Stoichiometry of the reaction:

1 mole of silver chloride produces 1 mole of chlorine ions

So, 0.00215 moles of silver chloride will produce =
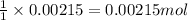`(1)/(1)* 0.00215=0.00215mol` of chloride ions

Mass of chloride ions =
`(0.00215mol* 35.45g/mol)=0.0762g`

Putting values in equation 2, we get:

`\text{Mass percent of chloride ion}=(0.0762g)/(0.256g)* 100\\\\\text{Mass percent of chloride ion}=29.76\%`

Mass percent of chloride ion = 29.76 %

• For
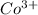  `Co^(3+)` ion:

Calculating moles of cobalt (III) oxide by using equation 1:

Moles of cobalt (III) oxide =
`(0.145g)/(165.86g/mol)=0.00087mol`

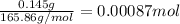
The chemical equation for the ionization of cobalt (III) oxide follows:

`Co_2O_3\rightarrow 2Co^(3+)+3O^(2-)`

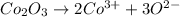
By Stoichiometry of the reaction:

1 mole of cobalt (III) oxide produces 2 moles of cobalt ions

So, 0.00087 moles of cobalt (III) oxide will produce =
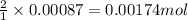`(2)/(1)* 0.00087=0.00174mol` of cobalt ions

Mass of cobalt ions =
`(0.00174mol* 117.86g/mol)=0.205g`

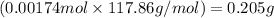
Putting values in equation 2, we get:

`\text{Mass percent of cobalt ion}=(0.205g)/(0.416g)* 100\\\\\text{Mass percent of cobalt ion}=49.28\%`

Mass percent of cobalt ion = 49.28 %

• For hydrogen and oxygen ion:

Calculating mass percent of water:

Mass percent of water = 100 - (29.76 + 49.28) = 20.96 %

Let the mass of compound be 100 grams. So, mass of water in the compound will be 20.96 g

For hydrogen:

In 18 grams of water, mass of hydrogen ion present is (1 × 2) = 2 g

So, in 20.96 grams of water, mass of hydrogen ion present will be =
`(2)/(18)* 20.96=2.33g`

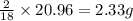
Putting values in equation 2, we get:

`\text{Mass percent of hydrogen ion}=(2.33g)/(100g)* 100\\\\\text{Mass percent of hydrogen ion}=2.33\%`

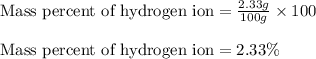
Mass percent of hydrogen ion = 2.33 %

For oxygen:

In 18 grams of water, mass of oxygen ion present is (16 × 1) = 16 g

So, in 20.96 grams of water, mass of oxygen ion present will be =
`(16)/(18)* 20.96=18.63g`

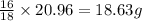
Putting values in equation 2, we get:

`\text{Mass percent of oxygen ion}=(18.63g)/(100g)* 100\\\\\text{Mass percent of oxygen ion}=18.63\%`

Mass percent of oxygen ion = 18.63 %

Hence, the mass percent of
`Co^(3+),Cl^(-),H^+\text{ and }O^(2-)` ions in the compound are 49.28 %, 29.79 %, 2.33 % and 18.63 % respectively