Answer: 11.24m
Step-by-step explanation:
Given that:
- initial velocity of first ball,
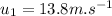
- initial velocity of second
 ( negative because thrown against the gravity)
( negative because thrown against the gravity)
- acceleration of gravity, g =
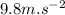
Using the equations of motion:
To find the final velocity after the given time 0.361 second.
 ................ (1)
................ (1)
where:
- v = final velocity of the body after time t under the influence of acceleration a (here g).
Putting the values of the respective balls
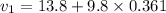
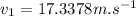
Similarly
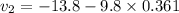 ∵the body is thrown against the gravity will have decelerating effect.
∵the body is thrown against the gravity will have decelerating effect.
 ∵the body is still moving up with this velocity
∵the body is still moving up with this velocity
Now, using the eq.
 .............................(2)
.............................(2)
where, the symbols have usual meaning as above and:
- s= distance covered by the body.
Putting the respective values in eq. (2)
For the body in the first case:
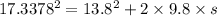
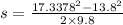
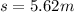
For the body in the second case:
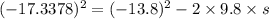
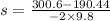
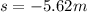
∴The bodies are
 apart from each other from the point from which they are thrown.
apart from each other from the point from which they are thrown.