Question

A) Show that z = 1 + i is a solution to the fourth degree polynomial equation z^4 − z^3 + 3z^2 − 4z + 6 = 0

b) Show that z = 1 − i is a solution to the fourth degree polynomial equation z^4 − z^3 + 3z^2 − 4z + 6 = 0.

Answer 1

Answer: The verification is done below.

Step-by-step explanation: We are given to show that x = 1+i and z= 1-i are the solutions to the following fourth degree polynomial equation :

`z^4-z^3+3z^2-4+6=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

z = a is a solution of a polynomial equation f(z) if f(a) = 0.

We will be using the following value of i(iota) :

`i=√(-1)~~~~~\Rightarrow i^2=-1.`

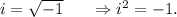
(a) Substituting z = 1+i in the left hand side of equation (i), we get

`z^4-z^3+3z^2-4z+6\\\\=(1+i)^4-(1+i)^3+3(1+i)^2-4(1+i)+6\\\\=(1+2i+i^2)^2-(1+2i+i^2)(1+i)+3(1+2i+i^2)-4-4i+6\\\\=(2i)^2-2i(1+i)+3*2i-4i+2\\\\=4i^2-2i+2+6i-4i+2\\\\=-4+4\\\\=0.`

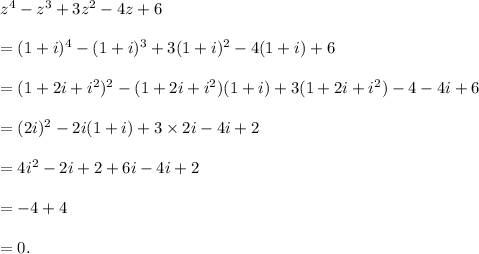
So, z = 1+i is a solution of the given polynomial equation.

(b) Similarly, substituting z = 1-i in the left hand side of equation (i), we get

`z^4-z^3+3z^2-4z+6\\\\=(1-i)^4-(1-i)^3+3(1-i)^2-4(1-i)+6\\\\=(1-2i+i^2)^2-(1-2i+i^2)(1-i)+3(1-2i+i^2)-4+4i+6\\\\=(-2i)^2+2i(1-i)+3*(-2i)+4i+2\\\\=4i^2+2i+2-6i+4i+2\\\\=-4+4\\\\=0.`

So, z = 1-i is a solution of the given polynomial equation.

Hence showed.