Answer:
- For the statement
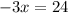 , the reason is: Subtraction property of Equality
, the reason is: Subtraction property of Equality
- For the statement
 , the reason is: Division property of Equality.
, the reason is: Division property of Equality.
- For the statement
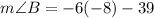 , the reason is: Substitution property of Equality.
, the reason is: Substitution property of Equality.
Explanation:
The missing pictures are attached.
We must remember that:
- The Subtraction property of Equality states that:
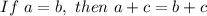
- The Division property of Equality states that:
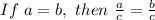
- The Substitution property of Equality states that:

Knowing this properties we can identify the missing reasons that correctly complete the proof.
- For the statement
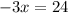 , the reason is:
, the reason is:
Subtraction property of Equality
(Because it is obtained by subtracting 66 from both sides of
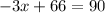 )
)
- For the statement
 , the reason is:
, the reason is:
Division property of Equality
(Because it is obtained by dividing both sides of
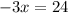 by -3)
by -3)
- For the statement
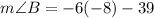 , the reason is:
, the reason is:
Substitution property of Equality
(Because it is obtained by substituting the value of "x" into
 )
)