Answer:
The series of nelsons debt balance is 450, 466.34, 474.74, 483.28 ……. Option D is correct.
Solution:
Given, Many credit card companies charge a compound interest rate of 1.8% per month on a credit card balance.
Means each month the rate increases exponentially.
Nelson owes $450 on a credit card and makes no purchases or payments, he will get into debt in the following way:
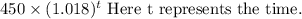
Because we know that, compound interest

$450 was initial amount.

Hence, the series of nelsons debt balance is 450, 466.34, 474.74, 483.28 …….
Thus option D is correct