Question

Which points are the best approximations of the relative maximum and minimum of the

function?
f(x) = x3 + 3x2 – 9x -8
The relative maximum is at (3, -13), and the relative minimum is at (-3, -19).
The relative maximum is at (-3, 19), and the relative minimum is at (1, -13).
The relative maximum is at (3, -13), and the relative minimum is at (3, -19).
The relative maximum is at (-3, -19), and the relative minimum is at (-1, -13).

Answer 1

B, The relative maximum is at (-3, 19), and the relative minimum is at (1, -13)

Explanation:

Answer 2

Function has relative maximum at point (-3,19) and relative minimum at (1,-13)

Explanation:

We are given that

`f(x)=x^3+3x^2-9x-8`

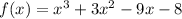
Differentiate w.r.t x

`f'(x)=3x^2+6x-9`

`f'(x)=0`

`3x^2+6x-9=0`

`x^2+2x-3=0`

`^2+3x-x-3=0`

`x(x+3)-1(x+3)=0`

`(x+3)(x-1)=0`

`x+3=0\implies x=-3`

`x-1=0\implies x=1`

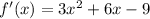
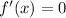
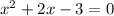
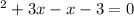
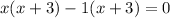
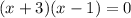
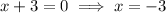
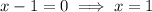
Substitute x=-3 then we get

Now we check for x<-3 -3<x<1 and x>1

For x<-3

Substitute x=-4

`f'(-4)=3(-4)^2+6(-4)-9=15`

f'(x)>0

Function is increasing

For -3<x<1

Substitute x=0

f'(0)=-9<0

Function is decreasing for -3<x<1

x>1

Substitute x=2

f'(2)=
`3(2)^2+6(2)-9=15>0`

Function is increasing

When sign of function changes from negative to positive then function has relative minimum.

When the sign of function changes from positive to negative then function has relative maximum .

Substitute x=1

f(1)=
`1+3-9-8=-13`

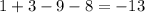
Substitute x=-3

f(-3)=
`(-3)^3+3(-3)^2-9(-3)-8=19`

Therefore, function has relative maximum at point (-3,19) and relative minimum at (1,-13)