Question

A farmer is going to divide her 50 acre farm between two crops. Seed for crop A costs $10 per acre. Seed for crop B costs $5 per acre. The farmer can spend at most $400 on seed. If crop B brings in a profit of $90 per acre, and crop A brings in a profit of $120 per acre, how many acres of each crop should the farmer plant to maximize her profit?

acres of crop A
acres of crop B

Answer 1

To maximize the profit, the farmer should plant 30 acres of crop A and 20 acres of crop B

Explanation:

Let

x -----> the number of acres of crop A

50-x ----> the number of acres of crop B

we know that

`10x+5(50-x) \leq 400`

`10x+250-5x \leq 400`

`10x-5x \leq 400-250`

`5x \leq 150`

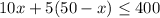
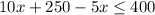
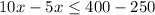
`x \leq 30` ----> inequality A

The maximum value of x is 30 acres

The profit is equal to

`P=120x+90(50-x)`

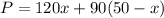
For x=30

Find the value of P

`P=120(30)+90(50-30)`

`P=120(30)+90(20)`

`P=\$5,400`

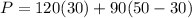
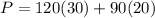
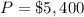
therefore

To maximize the profit, the farmer should plant 30 acres of crop A and 20 acres of crop B