Question

a 2.80 kg mass is dropped from a height of 4.50 m. find its kinetic energy(KE) when it is 1.50 m above the ground?

Answer 1

The Kinetic Energy of the mass at 1.5m is 82.32J. It is actually equivalent to the loss in Potential Energy.

Formulas:

Potential Energy = mgh

Kinetic Energy =
`(1)/(2)mv^(2)`

Third Equation of Motion ⇒ 2gS = Vf²-Vi²

While

m = mass of the object = 2.8kg

h = height of the object = 4.5m or 1.5m

v = velocity of the object

g = gravitational acceleration = 9.8m/s²

Steps:

Method 1

1. Finding Potential Energy at 4.5m. (K.E at this point will be zero because the body is stationary.)
2. Total P.E at 1.5m
3. Difference of Potential Energies i.e. Loss of potential energy will be Gain in Kinetic Energy.

Alternatively

1. Directly finding velocity at 1.5m height
2. Directly calculating Kinetic Energy at 1.5m by putting velocity as found in Step 1.

Explanation Method 1:

P.E at 4.5m

=mgh

=2.8x9.8x4.5

=123.48J

P.E at 1.5m

=mgh

=2.8x9.8x1.5

=41.16J

Loss in P.E = Gain in Kinetic Energy

Kinetic Energy = 123.48-41.16

=82.32J

Explanation Method 2:

Velocity at height 1.5m

Third equation of motion:

2gS = Vf²-Vi²

2x9.8x(4.5-1.5) = Vf²-0²

(as distance traveled by the object is 4.5-1.5, initial velocity of the object at 4.5m is zero)

Vf²=58.8 (m/s²)²

Now, as

Kinetic Energy =
`(1)/(2) mv^(2)`

`K.E = (1)/(2)*2.8*58.8`

K.E = 82.32J

Answer 2

82.32 J

Step-by-step explanation:

Given:

Mass,
`m=2.80\textrm{ kg}`

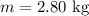
Initial height,
`h_(1)=4.50\textrm{ m}`

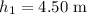
Final height,
`h_(2)=1.50\textrm{ m}`

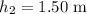
As the mass is dropped, its initial velocity is 0 m/s.

So, initial kinetic energy is also 0 J.

Now, according to conservation of energy,

Increase in Kinetic energy is equal to the decrease in potential energy.

Here, Decrease in potential energy is given as,

Δ
`PE=mg(h_(1)-h_(2))=2.8* 9.8(4.50-1.50)=82.32\textrm{ J}`

Now, increase in kinetic energy is equal to the kinetic energy at height
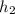`h_(2)` as the initial kinetic is 0.

∴ Kinetic energy at height 1.50 m above ground is given as the decrease in potential energy.

So, Kinetic energy = Decrease in potential energy =
`82.32\textrm{ J}`

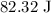
Kinetic energy at height 1.50 m above ground is
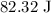`82.32\textrm{ J}`.